分形 · Pacyu

前言
#

话说一直想找时间写写关于学图形学时学到的东西，但又觉得码字好累（图形学中挺多公式和推导），这里先简单介绍一下如何使用 C/C++/Python 等语言画分形吧，其余的改天再补充。

数学家们对分形的研究也有很长时间了，著名的 Mandelbrot set、Julia set、Newton’s fractal 等，嘛，水平有限，只能从程序方面欣赏她的美了。

一些关于分形的网站： http://hpdz.net/

Mandelbrot set
#

C/C++：

#include <iostream>
#include <complex>

using std::complex;


uint8_t mandelbrot(complex<double> z, int max_iter)
{
	complex<double> c = z;
	for (int k = 0; k < max_iter; k++)
	{
		if (std::abs(z) > 2.) return k;
		z = std::pow(z, 2.) + c;
	}
	return max_iter;
}

int main()
{
	int w = 500, h = 500;
	double zoom_lx = -2., zoom_rx = 1.,
		zoom_ly = -1.5, zoom_ry = 1.5;
	int max_iter = 1000;
	FILE* fp = fopen("mandelbrot_frac_cpp.ppm", "wb");
	fprintf(fp, "P6 %d %d 255 ", w, h);
	for (int i = 0; i < h; i++)
	{
		double zy = zoom_ly + (double(i) / double(h - 1)) * (zoom_ry - zoom_ly);
		for (int j = 0; j < w; j++)
		{
			double zx = zoom_lx + (double(j) / double(w - 1)) * (zoom_rx - zoom_lx);
			complex<double> z(zx, zy);
			uint8_t n = mandelbrot(z, max_iter);
			double r = (108 * n) % 256,
				g = (88 * n) % 256,
				b = (245 * n) % 256;
			fprintf(fp, "%c%c%c", uint8_t(r), uint8_t(g), uint8_t(b));
		}
	}

	fclose(fp);
	return 0;
}

该代码会在执行文件同目录下生成一个 mandelbrot_frac_cpp.ppm 文件，linux系统可直接打开，windows系统上可使用一些转换工具，或者使用如下 python 脚本：

from PIL import Image
import sys

im = Image.open(sys.argv[1])
im.show()
im.save(open(sys.argv[2], 'wb'))

将上面脚本保存为 ppm2png.py 文件，然后命令行中运行：

py ppm2png.py mandelbrot_frac_cpp.ppm mandelbrot_frac_cpp.png

即可看到 png 格式的分形图像：

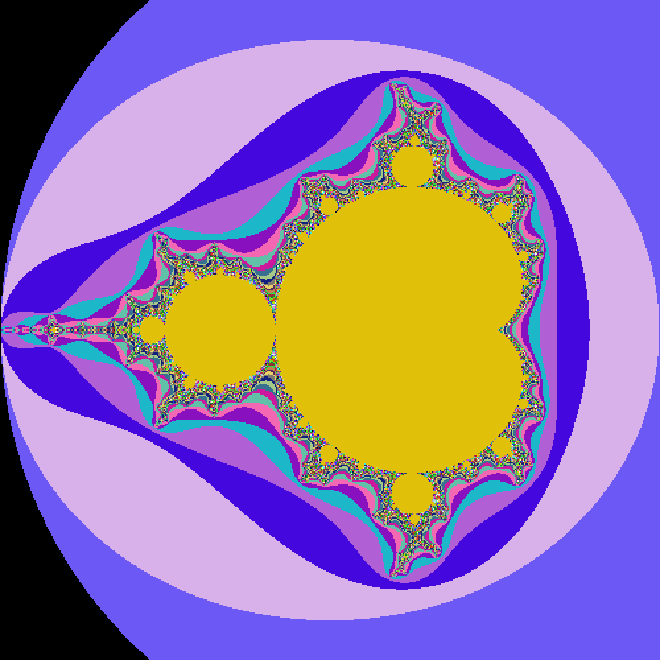
实际上我还没研究明白如何才能等比例无限放大 mandelbrot 分形的局部。

Python:

import numpy as np
import cv2 as cv

xa = -2.0
xb = 1.0
ya = -1.5
yb = 1.5

maxIt = 1000

imgx = 1200
imgy = 1200
image = np.zeros((imgx, imgy, 3), np.uint8)

for y in range(imgy):
    zy = y * (yb - ya) / (imgy - 1) + ya
    for x in range(imgx):
        zx = x * (xb - xa) / (imgx - 1) + xa
        z = zx + zy * 1j
        c = z
        i = 0
        while i < maxIt:
            if abs(z) > 2.0: break
            z = z * z + c
            i += 1
        r = i * 128 % 256
        g = i * 2 % 256
        b = i * 2 % 256
        image[y, x] = [int(b), int(g), int(r)]
cv.imwrite('mandelbort_frac_py.png', image)

该代码将输出一个 mandelbrot_frac_py.png 文件：

Newton fractal
#

这是一篇介绍牛顿迭代法的分形文章： https://www.chiark.greenend.org.uk/~sgtatham/newton/

这里画一个使用牛顿迭代 \( z = z^5 - 1 \) 的 \(5\) 个根所产生的分形图像。

C/C++:

#include <iostream>
#include <complex>

class Vec3b {
public:
	Vec3b(uint8_t r, uint8_t g, uint8_t b) : e{r, g, b} {}
	uint8_t r() { return e[0]; }
	uint8_t g() { return e[1]; }
	uint8_t b() { return e[2]; }
	uint8_t operator[](size_t i) { return e[i]; }
	uint8_t e[3];
}

auto fz = [](complex<double> z) { return std::pow(z, 5.) - complex<double>(1., 0.); };
auto dz = [](complex<double> z) { return 5. * std::pow(z, 4.); };

Vec3b fractal(size_t max_it, complex<double> z, complex<double> roots[], Vec3b color[])
{
	double a = -0.5;
	for (size_t k = 0; k < max_it; k++)
	{
		z -= fz(z) / dz(z);
		for (size_t r = 0; r < 5; r++)
		{
			complex<double> distance = z - roots[r];
			if (std::abs(distance) < 1e-6)
				return Vec3b(
					(color[r][0] * k) % 256,
					(color[r][1] * k) % 256,
					(color[r][2] * k) % 256);
		}
	}
	return color[5];
}

int main()
{
	size_t w = 500, h = 500;
	FILE* fp = fopen("picture.ppm", "wb");
	fprintf(fp, "P6 %d %d 255 ", w, h);
	
	complex<double> roots[5] = {
		complex<double>(1, 0),
		complex<double>(-(std::sqrt(5) + 1) / 4., -std::sqrt((5 - std::sqrt(5)) / 8.)),
		complex<double>((std::sqrt(5) - 1) / 4., std::sqrt((5 + std::sqrt(5)) / 8.)),
		complex<double>((std::sqrt(5) - 1) / 4., -std::sqrt((5 + std::sqrt(5)) / 8.)),
		complex<double>(-(1. + std::sqrt(5)) / 4., std::sqrt((5 - std::sqrt(5)) / 8.)),
	};
	
	Vec3b color[6] = {
		Vec3b(130, 18, 245),
		Vec3b(44, 245, 18),
		Vec3b(254, 183, 18),
		Vec3b(245, 14, 160),
		Vec3b(14, 121, 245),
		Vec3b(0, 0, 0)
	};
	
	for (size_t i = 0; i < h; i++)
	{
		double zy = 10. * (double(i) / double(h - 1)) - 5.;
		for (size_t j = 0; j < w; j++)
		{
			double zx = 10. * (double(j) / double(w - 1)) - 5.;
			complex<double> z(zx, zy);
			Vec3b c = fractal(100, z, roots, color);
			fprintf(fp, "%c%c%c", c.r(), c.g(), c.b());
		}
	}
	
	fclose(fp);
	return 0;
}