机器学习可以做许多有趣的事情,每个技术方向都有入门例子,但实际上只是照着入门例子抄,然后跑一遍可能对入门并没有帮助。于是我就个人入门经验,用自己的例子来做一个入门指导吧。
虽然是入门,但这里并不会指导进行环境搭建,所以,在看这篇文章之前,请先准备好机器学习的环境。
你将会了解到的 #
- 什么是数据集
- 如何训练模型
- 如何保存模型
- 模型的复用
什么是数据集 #
数据集一般也分为训练集和测试集,顾名思义,训练集用于训练,测试集用来测试训练好的模型的效果如何(有的数据集会包含验证集)。
首先我的例子是这样的:
预测方程 \( a_n = a_{n - 2} + a_{n - 4} + 1 \) 的第 \( n \) 项的值。(不要求答案完全正确,误差任意吧)
正常来说,这种问题不会用机器学习来做,明明可以写个递归跑,干嘛焉用牛刀,而且误差还很大?嘛…就当计算非常大的项 \( n \) 时,计算很慢,且只想知道值大概范围,那么你可以继续往下看。。。
我们需要有数据集,把数据喂给算法模型就是一个训练过程或者说算法的学习过程,那么如何制作数据集呢?
先考虑下面代码:
def recursive(x):
if x <= 2:
return 1
else:
return recursive(x - 2) + recursive(x - 4) + 1
直接把公式翻译成python代码,但当计算80+以上的项,python变得十分的慢,因为这是一个 n 次方时间复杂度的计算过程,有很多重复计算的部分,所以我们考虑优化成线性时间复杂度:
注意到奇数项 = 偶数项,所以我们只需要计算奇数项。偶数项则通过减 \( 1 \) 变为计算奇数项即可。而奇数项等于两个等差数列为 \( 2 \) 的更小的奇数项的和加 \( 1 \),即 \( a_n = a_{n-2} + a_{n-4} + 1 \),所以得到下面优化的线性时间复杂度的算法:
def r(n):
def it(a, b, i):
if i <= 2:
return a
elif i % 2 == 0:
return it(a, b, i - 1)
else:
return it(a + b + 1, a, i - 2)
return it(1, 1, n)
我们使用这个更快的算法来生成数据:
import pandas as pd
def r(n):
def it(a, b, i):
if i <= 2:
return a
elif i % 2 == 0:
return it(a, b, i - 1)
else:
return it(a + b + 1, a, i - 2)
return it(1, 1, n)
x = []
y = []
c = 1
for i in range(100):
x.append(i)
if i % 2 != 0:
c = r(i)
y.append(c)
save = pd.DataFrame({'data': x, 'result': y})
save.to_csv('train.csv', index=False)
这里我还做了一点处理,偶数项直接使用奇数项的,这样就不用再重复计算减 \1\ 的奇数项。
现在,数据准备好了,这里我选择0~80用来训练,80~100用来测试。你可以用两个文件中分别保存训练集和测试集,也可以把所有数据放在同一个文件,然后训练时只取一部分。我用了单个文件。
如何训练模型 #
前面也提到这是一个回归任务,虽然方法很多,那么至少应该要知道其中一种方法,可以用 sklearn 提供的 linear_model 来做一个简单的最小二乘法拟合数据。嘛,当然仅使用线性回归对于该问题是不合适的。
我们准备好需要导入的包:
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.linear_model import LinearRegression
from sklearn.externals import joblib
问题很单一,也限定了数据,所以我们不需要数据预处理。。。
可以先看看数据曲线,这是一种非常有用且直观的方法以了解数据:
data = pd.read_csv('train.csv')
sns.lmplot(x='data', y='result', data=data)
plt.show()
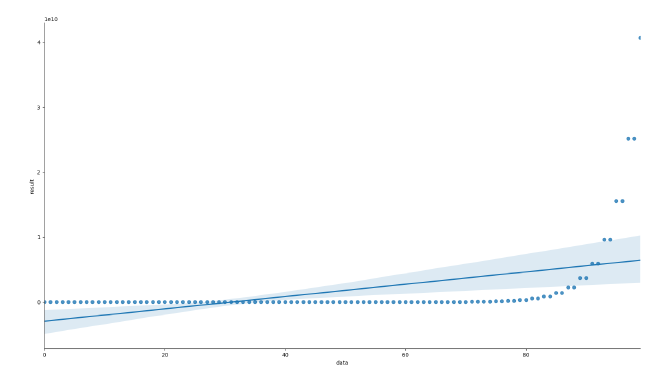
然后使用模型算法:
train_X, train_y = data.iloc[:, :-1].values, data['result']
clf = LinearRegression()
拟合数据:
clf.fit(train_X, train_y)
查看拟合系数:
print('参数:', clf.coef_)
对比源数据和预测结果:
fig, ax = plt.subplots()
ax.scatter(train_X, train_y, label='Origin data', c='orange')
ax.plot(train_X, clf.predict(train_X), label='Predict data')
ax.set_xlabel('data')
ax.set_ylabel('result')
ax.legend()
plt.show()
显然,非线性回归算法更合适,但这里我们学会了如何使用sklearn提供的工具来完成简单的回归任务。
保存模型 #
sklearn保存模型很简单(2020/12/04 更新:但似乎joblib功能要从sklearn中删除了,好久没用了。。):
joblib.dump(clf, 'save_model.m')
模型的复用 #
上面保存了训练好的模型,我们随时可以使用它:
test = pd.read_csv('test.csv')
test_X, test_y = test.iloc[:, :-1].values, test['result']
clf = joblib.load('save_model.m')
pred = clf.predict(test_X) # 预测
print(pred)
print('均方误差:%.2f' % mean_squared_error(y_true=test_y, y_pred=pred))
print('评分:%.2f' % r2_score(y_true=test_y, y_pred=pred))
完整代码 #
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.externals import joblib
data = pd.read_csv('train.csv')
sns.lmplot(x='data', y='result', data=data)
plt.show()
train_X, train_y = data.iloc[:, :-1].values, data['result']
clf = LinearRegression()
clf.fit(train_X, train_y)
print('参数:', clf.coef_)
fig, ax = plt.subplots()
ax.scatter(train_X, train_y, label='Origin data')
ax.plot(train_X, clf.predict(train_X), label='Predict data')
ax.set_xlabel('data')
ax.set_ylabel('result')
ax.legend()
plt.show()
joblib.dump(clf, 'save_model.m')
test = pd.read_csv('test.csv')
test_X, test_y = test.iloc[:, :-1].values, test['result']
clf = joblib.load('save_model.m')
pred = clf.predict(test_X) # 预测
print(pred)
print('均方误差:%.2f' % mean_squared_error(y_true=test_y, y_pred=pred))
print('评分:%.2f' % r2_score(y_true=test_y, y_pred=pred))

