数学-导数篇（持续更新）

这里主要存放一些导数题。

题目
#

1.已知向量 $ a = (\sin(x), \frac{3}{4}), b = (\cos(x), -1) $.

(1) 当 $ a // b $ 时，求 $ cos^2(x) - sin(2x) $；

(2) 设函数 $ f(x) = 2(\vec{a} + \vec{b}) \cdot \vec{b} $，已知在△ABC中，内角 $ A, B, C $ 的对边分别为 $ a, b, c $，若 $ a = \sqrt{3}, b = 2, \sin(B) = \frac{\sqrt{6}}{3} $，求 $ f(x) + 4 cos(2A + \frac{\pi}{6})(x \in [0, \frac{\pi}{3}]) $ 的取值范围。

题解：

(1) 求 $ \cos^2(x) - \sin(2x) $

由 $ a // b $，有 $ \tan(x) = -\frac{3}{4} $。

对 $ \cos^2(x) - \sin(2x) $ 做一些变形：

$$ \begin{aligned} \cos^2(x) - \sin(2x) &= \cos^2(x)(1 - \frac{\sin(2x)}{\cos^2(x)}) \\ &= \cos^2(x)(1 - \frac{2\sin(x)cos(x)}{\cos^2(x)}) \\ &= \cos^2(x)(1 - 2\tan(x)) \end{aligned} $$

然后考虑 $ \tan(x) = -\frac{3}{4} = \frac{\sin(x)}{\cos(x)} $

有以下情况：

$ \sqrt{(-3)^2 + 4^2} = 5 $ 或 $ \sqrt{3^2 + (-4)^2} = 5 $
$ \sin(x) $ 为负或者 $ \cos(x) $ 为负

既有 $ \cos(x) = -\frac{4}{5} $ 或者 $ \cos(x) = \frac{4}{5} $

这并不影响到 $ \cos^2(x) $ 的值，所以有

$$ \begin{aligned} \cos^2(x) - \sin(2x) &= \cos^2(x)(1 - 2\tan(x)) \ &= \frac{16}{25} \cdot [1 - 2 \cdot (-\frac{3}{4})] \ &= \frac{8}{5} \end{aligned} $$

(2) 求 $ f(x) + 4\cos(2A + \frac{\pi}{6}) (x \in [0, \frac{\pi}{3}]) $ 的取值范围

先求角 $ A $.

由正弦定理知：$ \sin(A) = \frac{a\sin(B)}{b} = \frac{\sqrt{3}\frac{\sqrt{6}}{3}}{2} = \frac{\sqrt{2}}{2} \rightarrow A = \frac{\pi}{4} $，所以 $ \cos(2A + \frac{\pi}{6}) = \cos(\frac{\pi}{2} + \frac{\pi}{6}) = -\sin(\frac{\pi}{6}) = -\frac{1}{2} $。

令 $ \varphi (x) = f(x) - 2 (x \in [0, \frac{\pi}{3}]) $

由题目条件知： $ f(x) = 2cos^2(x) + sin(2x) + \frac{1}{2} $

$$ \begin{aligned} f’(x) &= -4\cos(x)\sin(x) + 2\cos(2x) \ &= 2(\cos(2x) - \sin(2x)) \ &= 2\sqrt{2}\sin(-2x + \frac{\pi}{4}) \end{aligned} $$

令 $ f’(x) = 0 $，则可得到 $ x = \frac{\pi}{8} + k\pi (k = 0,1,2…) $

$ \because x \in [0, \frac{\pi}{3}], \therefore x = \frac{\pi}{8} $

① $ f’(x) $ 在 $ x \in [0, \frac{\pi}{8}) $ 恒大于 $ 0 $，原函数 $ f(x) $ 在 $ x \in [0, \frac{\pi}{8}) $ 内单调递增；$ f’(x) $ 在 $ x \in (\frac{\pi}{8}, \frac{\pi}{3}] $ 恒小于 $ 0 $，原函数 $ f(x) $ 在 $ x \in (\frac{\pi}{8}, \frac{\pi}{3}] $ 内单调递减，所以 $ x = \frac{\pi}{8} $ 为 $ f(x) $ 在 $ x \in [0, \frac{\pi}{3}) $ 内的唯一一个最大值.

② 因为 $ f(x) $ 在 $ (\frac{\pi}{8}, \frac{\pi}{3}] $ 上单调递减，又 $ f(0) > f(\frac{\pi}{3}) $，所以 $ f(\frac{\pi}{3}) $ 是 $ f(x) $ 在 $ x \in [0, \frac{\pi}{3}) $ 内的唯一一个最小值.

可以借助工具来画出函数图看一看是否正确：

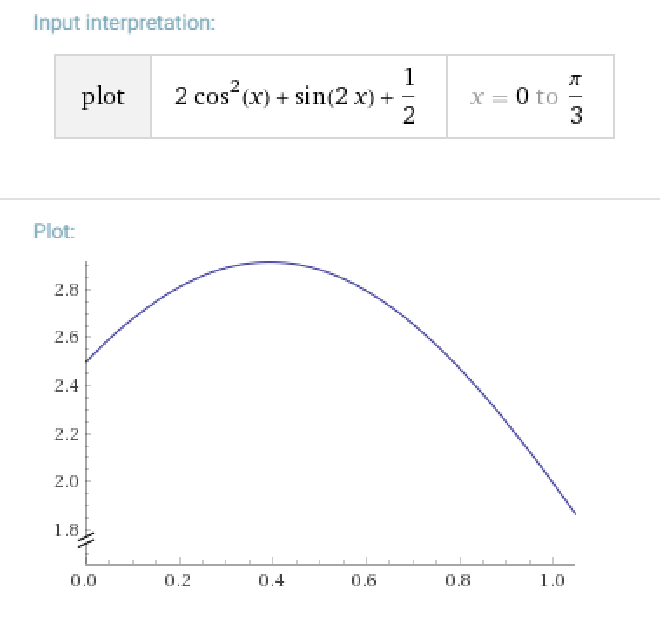
由计算可得 $ f(\frac{\pi}{8}) = \frac{3}{2} + \sqrt{2}, f(\frac{\pi}{3}) = 1 + \frac{\sqrt{3}}{2} $

于是

$$ \begin{aligned} max(\varphi(x)) &= f(\frac{\pi}{8}) - 2 = \sqrt{2} - \frac{1}{2} \ min(\varphi(x)) &= f(\frac{\pi}{3}) - 2 = \frac{\sqrt{3}}{2} - 1 \end{aligned} $$

2.(2019 全国卷Ⅲ 理数）已知函数 $ f(x) = 2x^3 - ax^2 + b $.

(1) 讨论 $ f(x) $ 的单调性;

(2) 是否存在 $ a, b $，使得 $ f(x) $ 在区间 $ [0, 1] $ 的最小值为 $ -1 $ 且最大值为 $ 1 $？若存在，求出 $ a, b $ 的所有值；若不存在，说明理由。

虽然是比较简单的题，不过还是给出题解吧：

(1) 显然，该题这类含未知量的函数要讨论单调性，利用求导工具最便利，对 $ f(x) $ 求导有：$ f’(x) = 6x^2 - ax $. 现在我们就只需要对 $ a $ 分类讨论函数的单调区间了。

① 当 $ a < 0 $

若 $ f’(x) \leq 0 $，有 $ \begin{aligned} 6x^2 - 2ax &\leq 0 \\ 2x \cdot (3x - a) &\leq 0 \end{aligned} $，解不等式得到：$ \frac{a}{3} \leq x \leq 0 $（注意 $ a < 0 $），即 $ f’(x) \ 在 \ [\frac{a}{3}, 0] $ 上小于 $ 0 $，而原函数 $ f(x) $ 在 $ [\frac{a}{3}, 0] $ 上单调递减.
若 $ f’(x) > 0 $，由 $ \begin{aligned} 6x^2 - 2ax &> 0 \ 2x \cdot (3x - a) &> 0 \end{aligned} $，得：$ x < \frac{a}{3}, x > 0 $，即 $ f’(x) $ 在 $ (-\infty, \frac{a}{3}) \vee (0, +\infty) $ 上大于 $ 0 $，而原函数 $ f(x) $ 在 $ (-\infty, \frac{a}{3}) \vee (0, +\infty) $ 上单调递增.

② 当 $ a = 0 $

$ a = 0 $，所以有 $ f’(x) = 6x^2 \geq 0 $，因此原函数 $ f(x) $ 在 $ (-\infty, +\infty) $ 上单调递增.

③ 当 $ a > 0 $

若 $ f’(x) \leq 0 $，由 $ \begin{aligned} 6x^2 - 2ax &\leq 0 \\ 2x \cdot (3x - a) &\leq 0 \end{aligned} $，得：$ 0 \leq x \leq \frac{a}{3} $，即 $ f’(x) $ 在 $ [0, \frac{a}{3}] $ 上小于 $ 0 $，而原函数 $ f(x) $ 在 $ [0, \frac{a}{3}] $ 上单调递减.
若 $ f’(x) > 0 $，由 $ \begin{aligned} 6x^2 - 2ax &> 0 \\ 2x \cdot (3x - a) &> 0 \end{aligned} $，得：$ x < 0 或 x > \frac{a}{3} $ ，即 $ f’(x) \ 在 \ (-\infty, 0) \vee (\frac{a}{3}, +\infty) $ 上大于 $ 0 $，而原函数 $ f(x) $ 在 $ (-\infty, 0) \vee (\frac{a}{3}, +\infty) $ 上单调递增.

讨论完毕。

(2) 只需要利用 (1) 讨论得结果即可证明。

① 当 $ a < 0 $，由 (1) 问知 $ f(x) $ 在 $ (0, +\infty) $ 上单调递增，那么函数 $ f(x) $ 可在端点处取得最小值和最大值，即

$$ \begin{aligned} min(f(x)) &= b = -1 \quad when \ x = 0 \\ max(f(x)) &= 2 - a + b \quad when \ x = 1 \end{aligned} $$

由 $ b = -1, max(f(x)) = f(1) = 2 - a - 1 = 1 - a $，又因为 $ a < 0 $，所以 $ f(1) > 1 $，这与题目条件矛盾。

② 当 $ a = 0 $，由 (1) 问知 $ f(x) $ 在 $ (-\infty, +\infty) $ 上单调递增，那么函数 $ f(x) $ 可在端点处取得最小值和最大值，即

$$ \begin{aligned} min(f(x)) &= b = -1 \quad when \ x = 0 \\ max(f(x)) &= 2 + b \quad when \ x = 1 \end{aligned} $$

由 $ b = -1, max(f(x)) = f(1) = 2 - 1 = 1 $，正好满足题目条件，故存在 $ a = 0, b = -1 $ 使得函数 $ f(x) $ 在区间 $ [0, 1] $ 上得最小值为 $ -1 $，最大值为 $ 1 $。

③ 当 $ a > 0 $，由 (1) 问知 $ f(x) $ 在 $ [0, \frac{a}{3}] $ 上单调递减，那么函数 $ f(x) $ 可在 $ x = 0 $ 处取得最大值，$ x = \frac{a}{3} $ 处取得最小值。

当 $ 0 < a < 3 $ 时，$ f(x) $ 在 $ [0, 1] $ 上有 $ \begin{aligned} max(f(x)) &= b = 1 \quad when \ x = 0 \\ min(f(x)) &= 2(\frac{a}{3})^3 - a(\frac{a}{3})^2 + b \quad when \ x = \frac{a}{3}\end{aligned} $，由 $ b = 1, 2(\frac{a}{3})^3 - a(\frac{a}{3})^2 + 1 = -1 \Rightarrow a = 3 \cdot 2^{\frac{1}{3}} $，即，取 $ a = 3 \cdot 2^{\frac{1}{3}} > 3 $，故矛盾。
当 $ a \geq 3 $ 时，$ f(x) $ 在 $ [0, 1] $ 上有 $ \begin{aligned} max(f(x)) &= b = 1 \quad when \ x = 0 \\ min(f(x)) &= 2 - a + b \quad when \ x = 1\end{aligned} $，由 $ b = 1 $，有 $ f(1) = 2 - a + 1 = -1 \Rightarrow a = 4 $，满足题目条件。

故当 $ a = 0, b = -1$ 或 $ a = 4, b = 1 $ 时，$ f(x) $ 在 $ [0, 1] $ 上取得最小值和最大值。

证毕。