这里存放一些积分方程题的题解。
题目 #
1.求 \( \int_{0}^{\frac{\pi}{4}} x \ \prod cos(\frac{x}{2^k}) dx \) (from MIT 2015 Integration Bee) (这个题是在youtube上看到的,解法也是视频中给出的)
题解:
注意到 \( \prod cos(\frac{x}{2^k}) = cos(\frac{x}{2}) \cdot cos(\frac{x}{2^2}) \cdot \cdot \cdot \)
利用 \( sin(2x) = 2sin(x)cos(x) \Rightarrow cos(x) = \frac{sin(2x)}{2sin(x)} \)
将上面第一个等式最右边按照上式规则写出来,有:
$$ cos(\frac{x}{2}) \cdot cos(\frac{x}{2^2}) \cdot cos(\frac{x}{2^2}) \cdots = \frac{sin(x)}{2sin(\frac{x}{2})} \cdot \frac{sin(\frac{x}{2})}{2sin(\frac{x}{2^2})} \cdot \frac{sin(\frac{x}{2^2})}{2sin(\frac{x}{2^3})} \cdots $$
观察等式右边发现,除第一项分子以外,后一项的分子总是能和前一项的分母约掉,于是我们可以得到这样的形式:
$$ \frac{sin(x)}{2^k sin(\frac{x}{2^k})}, k \rightarrow \infty $$
于是,求极限:
$$ \begin{aligned} \lim_{k \rightarrow \infty} \frac{sin(x)}{2^k sin(\frac{x}{2^k})} &= sin(x) \lim_{k \rightarrow \infty} \frac{1}{2^k sin(\frac{x}{2^k})} \\ &= sin(x) \lim_{k \rightarrow \infty} \frac{1}{x\frac{sin(\frac{x}{2^k})}{\frac{x}{2^k}}} \\ &= sin(x) \lim_{k \rightarrow \infty} \frac{1}{x \cdot 1} \\ &= \frac{sin(x)}{x} \end{aligned} $$
所以,积分方程中的那一坨 \( \prod cos(\frac{x}{2^k}) = \frac{sin(x)}{x} \)
带入积分方程并计算:
$$ \begin{aligned} \int_{0}^{\frac{\pi}{4}} x \ \prod cos(\frac{x}{2^k}) dx &= \int_{0}^{\frac{\pi}{4}} x \ \frac{sin(x)}{x} dx \\ &= \int_{0}^{\frac{\pi}{4}} sin(x) dx \\ &= -cos(x)|{0}^{\frac{\pi}{4}} \\ &= -cos(\frac{\pi}{4}) - (-cos(0)) \\ &= 1 - \frac{\sqrt{2}}{2} \end{aligned} $$
2.求 \( \int_{0}^{\infty} x \ e^{1-x} + \left \lfloor x \right \rfloor e^{1-\left \lfloor x \right \rfloor} dx \) 的值(解法参考同上)
题解:
$$ \int_{0}^{\infty} x \ e^{1-x} + \left \lfloor x \right \rfloor e^{1-\left \lfloor x \right \rfloor} dx = \int_{0}^{\infty} x \ e^{1-x} dx + \int_{0}^{\infty} \left \lfloor x \right \rfloor e^{1-\left \lfloor x \right \rfloor} dx $$
等式右边第一项积分很好算:
$$ \begin{aligned} \int_{0}^{\infty} x \ e^{1-x} dx &= e\int_{0}^{\infty} x \ e^{-x} \\ &= e(-x \ e^{-x}|0^{\infty} - e^{-x}|0^{\infty}) \\ &= e[-e^{-x}(1+x)|{0}^{\infty}] \\ &= e \end{aligned} $$
现在来计算一下等式右边第二项积分:
令 \( S = \int_{0}^{\infty} \left \lfloor x \right \rfloor e^{1-\left \lfloor x \right \rfloor} dx \)
我们来看一下 \( f(x) = \left \lfloor x \right \rfloor e^{1-\left \lfloor x \right \rfloor} \) 的函数图:
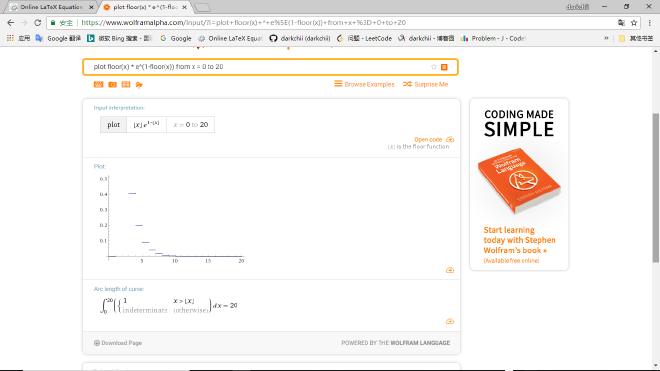
然后写几项看看,我们会发现可以用简单的级数形式来表示:
$$ \begin{aligned} S &= 0 \cdot 1 + 1 \cdot 1 + 2 \cdot \frac{1}{e} + 3 \cdot \frac{1}{e^2} + \cdots \\ &= 1 + \frac{2}{e} + \frac{3}{e^2} + \cdots \\ &= \sum_{x=0}^{\infty} \frac{x}{e^{x-1}} \end{aligned} $$
现在来求这个级数的和:
$$ \begin{aligned} S &= 1 + \frac{2}{e} + \frac{3}{e^2} + \cdots \quad (1) \\ \frac{1}{e} \cdot S &= \frac{1}{e} + \frac{2}{e^2} + \frac{3}{e^3} + \cdots \quad (2) \end{aligned} $$
\( (1) - (2) \)式有:
$$ \begin{aligned} S - \frac{1}{e} \cdot S &= 1 + \frac{1}{e} + \frac{1}{e^2} + \frac{1}{e^3} + \cdots \\ &= \sum_{n=0}^{\infty} (\frac{1}{e})^n \\ (1-\frac{1}{e})S &= \frac{1}{1-\frac{1}{e}} \\ \Rightarrow S &= \frac{1}{(1-\frac{1}{e})^2} \end{aligned} $$
回到原题 \( \int_{0}^{\infty} x \ e^{1-x} + \left \lfloor x \right \rfloor e^{1-\left \lfloor x \right \rfloor} dx = e + \frac{1}{(1-\frac{1}{e})^2} \)

