生活中许多实际应用都需要使用有向无环图来指明事件的优先次序。比如我们早上起床穿衣洗漱的次序等。 借用《算法导论》中举的例子,我制作了一张相同的图来描述这个概念:
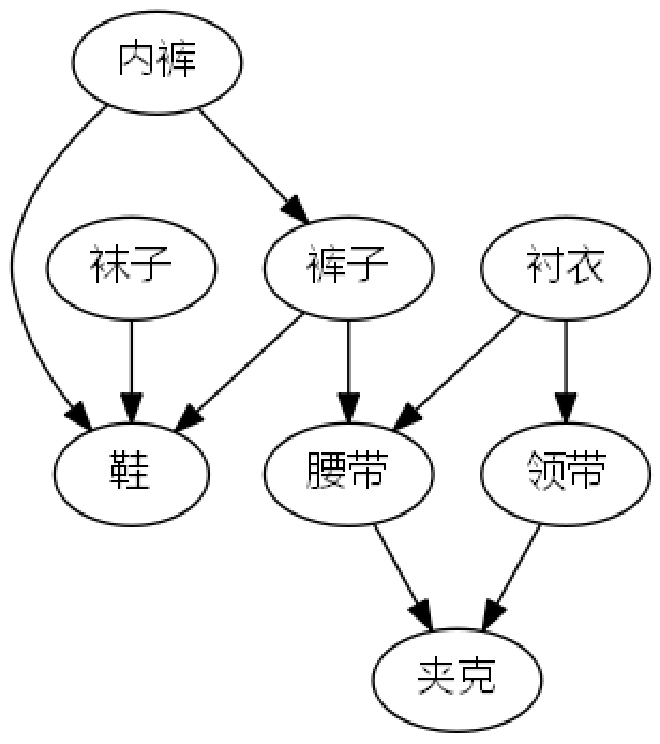
上图描述了,一个教授每天早上起床穿衣所发生的事件的次序图。教授必须先穿上某些衣物,才能再穿其他衣服(比如先穿上袜子才能再穿鞋子)。有些服饰则无先后次序,可以按任意顺序穿上。
如果我们按照教授每件衣物穿好时的时间排序,然后得到逆序,我们就可以看到教授的穿戴顺序,这样一个顺序就是拓扑排序。所以,拓扑排序的概念很简单。
但需要注意的是这样的事情必须发生在有向无环图中,假如有环,我们可以想象,教授这一些列动作是不可能完成的。
算法思路 #
如上面所说,我们的目的就是记录每个物件穿戴完成的时间,也就是在一个有向无环图中记录遍历过的每一个顶点v的离开时间,这只需要额外的一个 \( O(V) \) 空间消耗。
算法实现 #
#include <bits/stdc++.h>
#define INF 0x3f3f
int visied[INF], graph[INF][INF];
int d[INF], f[INF]; // 访问前的时间,访问后的时间,记录整个任务过程的时间线
int V, t = 0; // t表示时间
void dfs(int v)
{
t += 1;
d[v] = t;
visied[v] = 1;
for (int i = 1; i <= V; i++)
if (!visied[i] && graph[v][i])
dfs(i);
t += 1;
f[v] = t;
}
void topological_sort()
{
// sort to array f
}
int main()
{
int E, s, e;
scanf("%d %d", &V, &E);
memset(visied, 0, sizeof(visied));
memset(d, 0, sizeof(d));
memset(f, 0, sizeof(f));
for (int i = 0; i < E; i++)
{
scanf("%d %d", &s, &e);
graph[s][e] = 1;
}
for (int i = 1; i <= V; i++)
if (!visied[i])
dfs(i);
for (int i = 1; i <= V; i++)
printf("%d: %d\n", i, f[i]);
return 0;
}
测试用例如图:
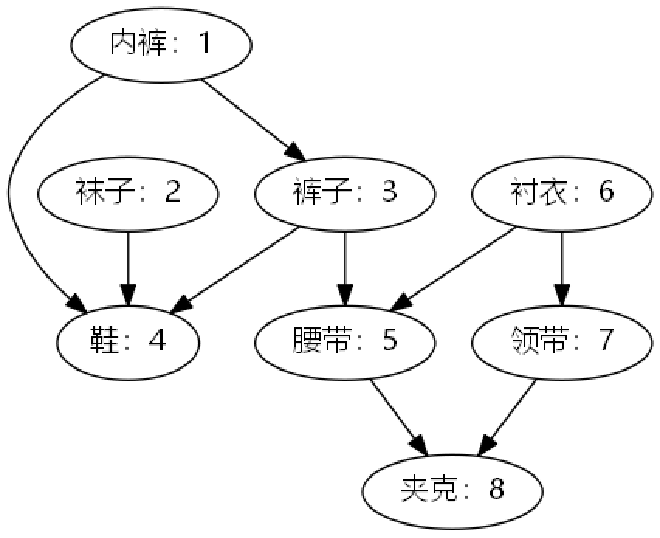
输出:
1: 10
2: 12
3: 9
4: 4
5: 8
6: 16
7: 15
8: 7
按时间逆序排序,看看顶点访问顺序:
6 7 2 1 3 8 5 4
结合前面的拓扑排序概念,可以证明这个排序是合理的。
时间复杂度分析 #
这是用邻接矩阵表示法实现的,所以排序时间复杂度为 \( O(V lg V) \),如果节点并不多可以使用一些空间换时间的排序手段降低排序时间。
参考 #
- 算法导论

