该算法可以用来求解一个有向图的强连通分量。
算法解析 #
什么是强连通分量?
先说说强连通图:在有向图 \( G \) 中,如果任意 \( u,v \) 两顶点间连通,则称 \( (u,v) \) 强连通,则图 \( G \) 的一个强连通图,强连通图的极大强连通子图(强连通分量)就是其本身。
根据上面的说法,如果向图 \( G \) 中添加 \( x \) 个额外节点,使得有向图 \( G \) 不再是强连通图,则存在强连通分量。
下面考虑下图
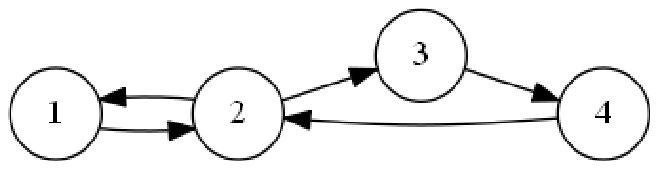
(不知道怎么用graphviz把节点位置弄得更好看一点,将就着看吧)
手工字符版:
1 <--> 2 --> 3
↖ |
\ ↓
4
该图的强连通分量个数为: \( 1 \) ,因为任意两顶点都能相互到达。
再举例:
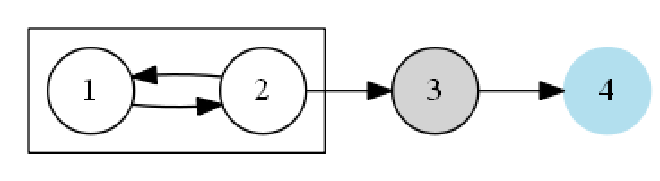
1 <--> 2 --> 3
|
↓
4
该图的强连通分量个数为:\( 3 \),图中\( (1,2)、(3)、(4) \)都是强连通分量。
明白了强连通分量后,再来看算法。
以

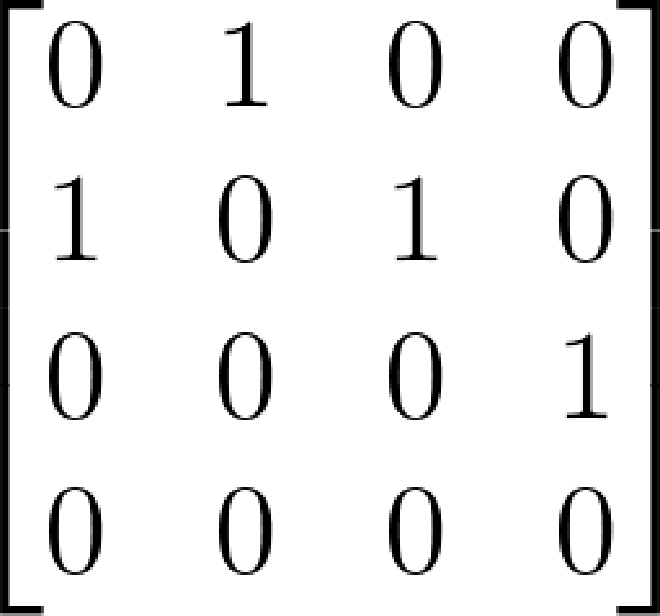
它的逆图及邻接矩阵:
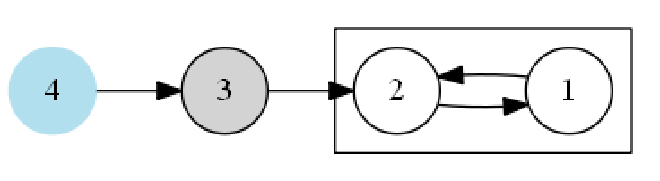
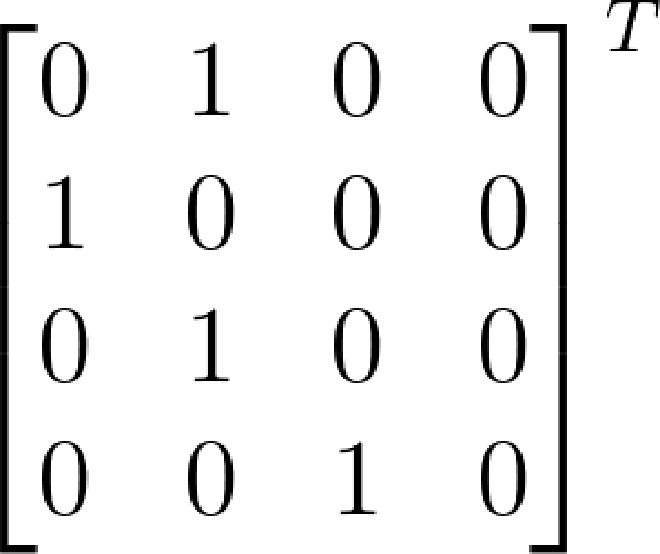
算法首先对原图进行 \( DFS \) 遍历,然后将所有顶点加入到栈中,然后再将栈中的顶点倒出,从倒出的顶点对逆图进行遍历,如果任意两顶点相连通,则 \( DFS2 \) 只调用一次就可以遍历逆图中所有顶点。如果出现不相互连通的顶点,则对逆图的遍历就会在中途中止,并通过栈中倒出的顶点来遍历完所有顶点。
现在来考虑核心算法部分的最坏情况的时间复杂度。
最坏情况时,显然所有顶点都是孤立的,算法开始时调用memset(),耗费 \( O(V) \),接下来调用DFS1(),无论原图是否为强连通图,DFS1()都将耗费 \( O(V^2) \),然后再次调用memset(),耗费 \( O(V) \),最后while()循环在最坏情况下将对每个顶点调用一次DFS2(),耗费 \( O(V^2) \)。所以算法的时间总消耗为 \( O(V + V^2 + V + V^2) = O(V^2) \),这是使用邻接矩阵表示图时的时间复杂度。
使用邻接链表表示图时的时间复杂度为 \( O(V + E) \) 的线性时间。
算法实现 #
#include <iostream>
#include <stack>
using namespace std;
int map[511][511];
int nmap[511][511];
int visited[501];
stack<int> S;
int N;
void DFS1(int v)
{
visited[v] = 1;
for (int i = 1; i <= N; i++)
if (!visited[i] && map[v][i])
DFS1(i);
S.push(v);
}
void DFS2(int v)
{
visited[v] = 1;
for (int i = 1; i <= N; i++)
if (!visited[i] && nmap[v][i])
DFS2(i);
}
int kosaraju()
{
memset(visited, 0, sizeof(visited));
for (int i = 1; i <= N; i++)
if (!visited[i]) DFS1(i);
int t = 0;
memset(visited, 0, sizeof(visited));
while (!S.empty())
{
int v = S.top();
S.pop();
// printf("|%d|", v);
if (!visited[v])
{
t++;
DFS2(v);
}
}
return t;
}
int main()
{
int M, s, e;
scanf_s("%d %d", &N, &M); // 顶点及边个数
memset(map, 0, sizeof(map));
memset(nmap, 0, sizeof(nmap));
for (int i = 0; i < M; i++)
{
scanf_s("%d %d", &s, &e);
map[s][e] = 1;
nmap[e][s] = 1;
}
printf("\n%d\n", kosaraju());
return 0;
}

