↓跳过正文
Pacyu
  1. Docs/

梯度下降算法（更新于 2020/12/04）

·1749 字·4 分钟· loading · loading · · ·
Algorithms Math C/C++ MatLab Python
Pacyu
作者
Pacyu
程序员
目录

梯度下降法(Gradient descent)又叫最速下降法，是一种局部搜索算法，属于智能算法，类似的有爬山算法、模拟退火等。基本原理是优化理论中的无约束问题，利用梯度搜索函数变化最快的方向，然后不断迭代寻找出极值的方法。

有空我将补上推导过程并给出梯度法的收敛条件，可能还会介绍一些其它无约束问题的优化算法(牛顿法、共轭梯度法等)及其他约束问题的优化算法，届时我们将会看到许多有趣的搜索算法，比如斐波那契法、黄金比例法（\\( 0.618 \\)法）等。

代码实现
#

使用方法就是自定义一个多元函数 \\( g \\)，然后如下方式调用：

(gradient-descent g init-arguments max-iterations tolerance)

例子： \\( f(x_1, x_2) = exp(x_1^2 + x_2^2) \\)

(gradient-descent
  (lambda (vec)
    (exp (+ (square (list-ref vec 0)) (square (list-ref vec 1)))))
  (list 1.0 1.0)
  30 0.00001)

Scheme
# 

(define delta 0.00001)

(define (deriv g)
  (lambda (x)
    (/ (- (g (+ x delta)) (g x))
       delta)))

(define (newton-transform g)
  (lambda (x)
    (- x (/ (g x) ((deriv g) x)))))

(define (fixed-point g first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) delta))
  (define (try guess)
    (let ((next (g guess)))
      (if (close-enough? guess next)
   guess
   (try next))))
  (try first-guess))

(define (newton-method g guess)
  (fixed-point (newton-transform g) guess))

(define (minimized g)
  (newton-method (deriv g) 1.0))

(define (gradient-descent g init-vec max-it tolerance)
  (define len (- (length init-vec) 1))
  (define (partial-derivative g)
    (lambda (vec index)
      (let ((d-vec (list-copy vec)))
 (list-set! d-vec index (+ (list-ref d-vec index) delta))
 (/ (- (g d-vec) (g vec)) delta))))
  (define (gradient-vector g vec)
    (define (iter i res)
      (if (< i 0)
   res
   (iter (- i 1) (cons ((partial-derivative g) vec i) res))))
    (iter len ()))
  (define (distance vec)
    (define (iter i result)
      (if (< i 0)
   result
   (iter (- i 1) (+ result (square (list-ref vec i))))))
    (sqrt (iter len 0)))
  (define (next vec x grad)
    (define (iter i res)
      (if (< i 0)
   res
   (iter (- i 1) (cons (- (list-ref vec i) (* x (list-ref grad i))) res))))
    (iter len ()))
  (define (x-transform vec x grad)
    (next vec x grad))
  (define (iter vec i)
    (let ((grad-vec (gradient-vector g vec)))
      (display vec)
      (newline)
      (cond ((< max-it i) vec)
     ((< (distance grad-vec) tolerance) vec)
     (else (let ((minimum (minimized
      (lambda (x)
        (g (x-transform vec x grad-vec))))))
      (iter (next vec minimum grad-vec) (+ i 1)))))))
  (iter init-vec 0))

C++
# 

#include <cmath>
#include <iostream>
#include <vector>
#include <cassert>
#include <functional>

const double h = 1e-5;

auto square(double x) -> double const { return x * x; }
auto cube(double x) -> double const { return x * x * x; }

template<class Fn_Ty>
auto partial_derivative(Fn_Ty g) {
    auto a = [g](const auto& vec, size_t i)
    {
        auto components = vec;
        components[i] += h;
        return (g(components) - g(vec)) / h;
    };
    return a;
}

template<class Fn_Ty, class Arg>
auto fixed_point(Fn_Ty g, Arg first_guess)
{
    auto close_enough = [](auto v1, auto v2)
    {
        return (std::abs(v1 - v2) < 1e-5);
    };
    auto try_again = [g, close_enough](auto guess, auto& try_ref)
    {
        auto next = g(guess);
        if (close_enough(guess, next)) return next;
        else return try_ref(next, try_ref);
    };
    return try_again(first_guess, try_again);
}

template<class Fn_Ty>
auto deriv(Fn_Ty g)
{
    auto a = [g](auto x)
    {
        return (g(x + h) - g(x)) / h;
    };
    return a;
}

template<class Fn_Ty>
auto newton_transform(Fn_Ty g)
{
    auto a = [g](auto x)
    {
        return x - (g(x) / deriv(g)(x));
    };
    return a;
}

template<class Fn_Ty, class Arg>
auto newton_method(Fn_Ty g, Arg guess)
{
    return fixed_point(newton_transform(g), guess);
}

std::vector<double> operator*(double b, const std::vector<double>& a)
{
    std::vector<double> c(a.size());
    for (size_t i = 0; i < a.size(); i++) c[i] = a[i] * b;
    return c;
}

std::vector<double> operator*(const std::vector<double>& a, double b)
{
    return b * a;
}

std::vector<double> operator-(const std::vector<double>& a, double b)
{
    std::vector<double> c(a.size());
    for (size_t i = 0; i < a.size(); i++) c[i] = a[i] - b;
    return c;
}

std::vector<double> operator-(double b, const std::vector<double>& a)
{
    std::vector<double> c(a.size());
    for (size_t i = 0; i < a.size(); i++) c[i] = b - a[i];
    return c;
}

std::vector<double> operator-(const std::vector<double>& a)
{
    std::vector<double> c(a.size());
    for (size_t i = 0; i < a.size(); i++) c[i] = -a[i];
    return c;
}

void operator+=(std::vector<double>& a, const std::vector<double>& b)
{
    assert(a.size() == b.size());
    for (size_t i = 0; i < a.size(); i++) a[i] += b[i];
}

void operator-=(std::vector<double>& a, const std::vector<double>& b)
{
    assert(a.size() == b.size());
    for (size_t i = 0; i < a.size(); i++) a[i] -= b[i];
}

template<class Goal_FnTy>
class GradientDescent {
public:
    GradientDescent(std::function<Goal_FnTy> g, std::vector<double> init_values, const double error, size_t max_iter = 20) :
        error(error), max_it(max_iter), gradient_components(), init_variable(init_values), vec(init_values), goal_fn(g)
    {
    }

    void run(bool output = true)
    {
        size_t step = 0;
        while (step < max_it)
        {
            if (output) step_output(step);

            std::vector<double> gradient_components; // 梯度向量
            for (size_t i = 0; i < vec.size(); i++)
                gradient_components.push_back(partial_derivative(goal_fn)(vec, i));

            if (distance(gradient_components) < error) break;

            auto fg = [this, gradient_components](auto lambda)
            {
                std::vector<double> lambda_components;
                for (size_t i = 0; i < vec.size(); i++)
                    lambda_components.push_back(vec[i] - lambda * gradient_components[i]);
                return goal_fn(lambda_components);
            };

            // 使用牛顿法搜索极小点
            double min_lambda = minimization(fg);    // 极小点
            vec -= gradient_components * min_lambda; // 下一步迭代
            step += 1;
        }
    }

    std::vector<double>& const run() const
    {
        run(false);
        return vec;
    }

    std::vector<double>& const get() const
    {
        return vec;
    }
    
private:
    void step_output(size_t step)
    {
        std::cout << step << " : " << "(";
        for (size_t i = 0; i < vec.size(); i++)
            std::cout << vec[i] << (i + 1 == vec.size() ? "" : ", ");
        std::cout << ")" << std::endl;
    }

    double distance(const std::vector<double>& vec)
    {
        double sum = 0;
        for (auto _ : vec) sum += square(_);
        return std::sqrt(sum);
    }

    template<class Fn_Ty>
    auto minimization(Fn_Ty g)
    {
        return newton_method(deriv(g), 1.0);
    }

    // 误差
    const double error;
    // 最大迭代次数
    size_t max_it;
    // 初始值
    std::vector<double> init_variable;
    // 最终目标函数极值
    std::vector<double> vec;
    // 目标函数
    std::function<Goal_FnTy> goal_fn;
};

测试
#

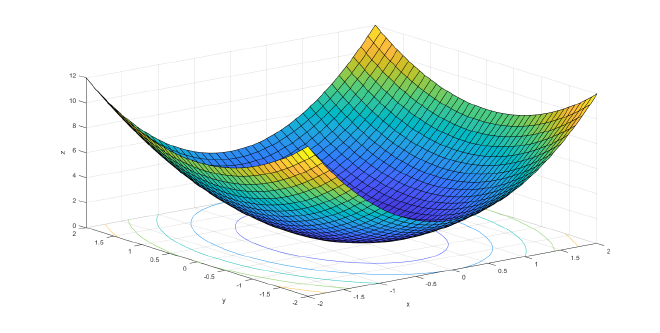
$$ min \ f(\mathbf{x}) = 2x_1 ^2 + x_2 ^2, \\ x_0 = (1, 1)^T, \epsilon = \frac{1}{100000} $$

问题最优解：(0, 0)

该函数的样子：

f(x) = 2x_1 ^2 + x_2 ^2

Scheme：

(gradient-descent (lambda (vec) (+ (* 2 (square (list-ref vec 0))) (square (list-ref vec 1)))) (list 1.0 1.0) 20 0.00001)

输出：

(1. 1.)
(-.11109809785453906 .44445095107273047)
(.07406415148073814 .0740568166924851)
(-8.226060108502659e-3 3.2915785342297756e-2)
(5.479613029965878e-3 5.473976292833832e-3)
(-6.076458754474259e-4 2.4334748892817517e-3)
(3.998023673891758e-4 3.952652685951883e-4)
(-4.351939188329914e-5 1.760888045421857e-4)
(2.3048444806604486e-5 1.9613203841429633e-5)
(-1.9005725715702401e-6 8.666514023037452e-6)
(-4.13145223743898e-6 3.7481300728847094e-6)
(-4.519310966043615e-6 1.7948473900002134e-6)
(-4.58949997889981e-6 1.2987640626074323e-6)
(-4.602395677437769e-6 1.1998274507463487e-6)
(-4.604772161673363e-6 1.1812992414638758e-6)
(-4.605206860686667e-6 1.1778999304581313e-6)
(-4.605288702309115e-6 1.1772595832695892e-6)
(-4.605301020582233e-6 1.1771631923490466e-6)
(-4.6053101069904185e-6 1.1770920897757949e-6)
(-4.605310439480507e-6 1.1770894879586069e-6)
(-4.6053066942518565e-6 1.177118795311575e-6)
(-4.605302200151839e-6 1.1771539626038494e-6)
;Value: (-4.605302200151839e-6 1.1771539626038494e-6)

C++：

int main()
{
    auto my_func = [](const auto& x)
    {
        return 2. * square(x[0]) + square(x[1]);
    };
    
    GradientDescent<double(const std::vector<double>&)> gd = GradientDescent<double(const std::vector<double>&)>(my_func, {1.0, 1.0}, 1e-5);
    gd.run();
    return 0;
}

输出：

0 : (1, 1)
1 : (-0.111091, 0.444454)
2 : (0.074063, 0.0740505)
3 : (-0.00822527, 0.0329133)
4 : (0.00547914, 0.00547344)
5 : (-0.000607558, 0.00243326)
6 : (0.000399758, 0.0003952)
7 : (-4.35106e-05, 0.000176061)
8 : (2.30431e-05, 1.9607e-05)
9 : (-1.89989e-06, 8.6636e-06)
10 : (-4.13021e-06, 3.74858e-06)
11 : (-4.51828e-06, 1.79693e-06)
12 : (-4.58859e-06, 1.3009e-06)
13 : (-4.60152e-06, 1.20187e-06)
14 : (-4.60391e-06, 1.18329e-06)
15 : (-4.60435e-06, 1.17985e-06)
16 : (-4.60443e-06, 1.17921e-06)
17 : (-4.60445e-06, 1.17909e-06)
18 : (-4.60445e-06, 1.17907e-06)
19 : (-4.60445e-06, 1.17907e-06)

其它语言实现
#

Matlab
# 

clc;clear;
figure

f = @(x,y) 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ... 
   - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ... 
   - 1/3*exp(-(x+1).^2 - y.^2);

tolerance = 1e-5;
max_iter = 30;

x0 = 0.;
y0 = 1.5;
x = -2.8:0.001:2.8;
y = x';
X = -2.8:0.05:2.8;
set(gcf, 'Position', get(0,'Screensize'));
surf(X,X,f(X, X'));
xlabel('x');ylabel('y');zlabel('z');
[gx,gy] = gradient(f(x, y), 0.1);
hold on
filename = 'd:/blog/img/gradient_descent_visualization.gif';
for i=0:1:max_iter
%     syms x y
%     g = gradient(f, [x, y]);
%     g1 = subs(g(1), [x, y], {x0, y0});
%     g2 = subs(g(2), [x, y], {x0, y0});
%     d = -[g1 g2];
    t = find(((x < x0 + 1e-3) & (x > x0 - 1e-3)) & ((y < y0 + 1e-3) & (y > y0 - 1e-3)));
    d = [gx(t), gy(t)];
    disp(d)
    if isempty(d)
        break;
    elseif(sqrt(d * d') < tolerance)
        break;   
    end
    plot3(x0,y0,f(x0, y0),'r*');
    lambda = fminbnd(@(c) f(x0 - c*d(1), y0 - c*d(2)), -5, 5);
    x0 = x0 - lambda*d(1);
    y0 = y0 - lambda*d(2);
    drawnow
    
    frame = getframe(gcf);
    im = frame2im(frame);
    [imind,cm] = rgb2ind(im,256);
    if i == 0
        imwrite(imind,cm,filename,'gif', 'Loopcount',inf);
    else
        imwrite(imind,cm,filename,'gif','WriteMode','append');
    end
end

输出：

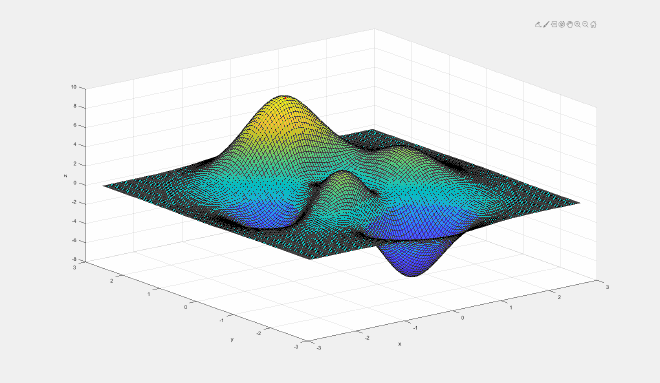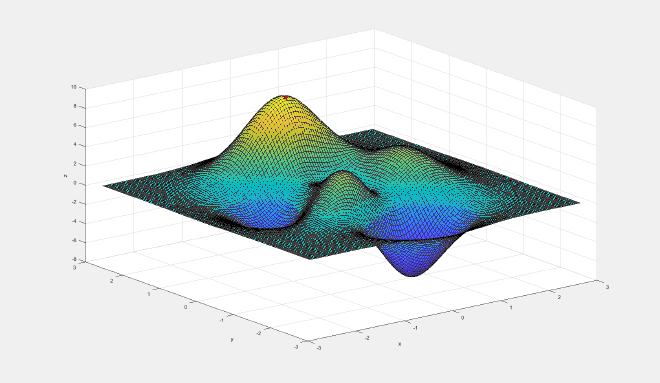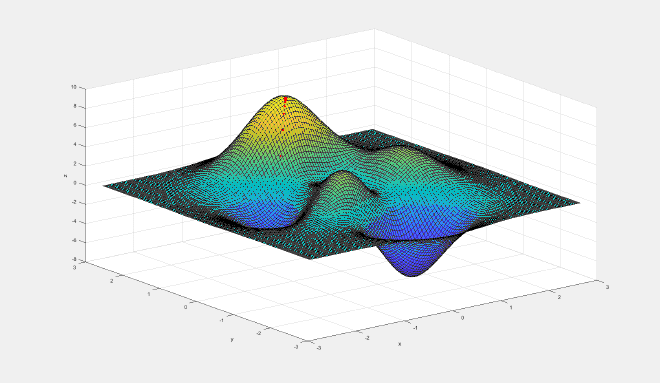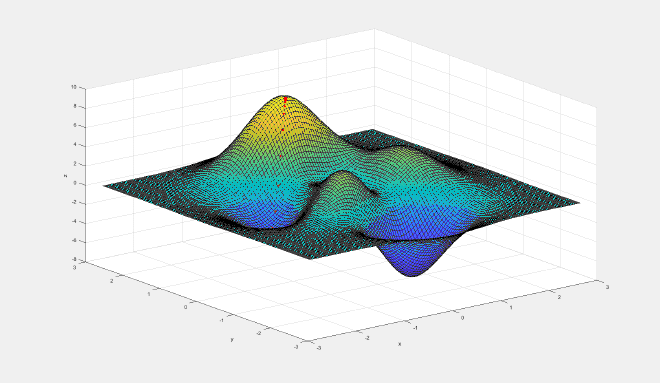
梯度下降可视化

以下部分是以前写的，暂时没更新。

Python
# 

square = lambda x: x ** 2
side = lambda a, b: (a ** 2 + b ** 2) ** (1 / 2)


def d(x_1, x_2):
    return -4 * x_1, -2 * x_2

def evaluate(x_1, x_2, a, b):
    return -(2 * a * x_1 + b * x_2) / (2 * square(a) + square(b))

def gradient_descent(x_1, x_2, epsilon, max_iters):
    iters = 0
    a, b = 1, 1
    while (side(a, b) > epsilon) & (iters < max_iters):
        print('%d (%.6f, %.6f)' % (iters + 1, x_1, x_2))
        a, b = d(x_1, x_2)
        gamma = evaluate(x_1, x_2, a, b)
        (x_1, x_2) = (x_1 + a * gamma, x_2 + b * gamma)
        iters += 1


if __name__ == '__main__':
    gradient_descent(1, 1, 0.001, 100)

输出:

1 (1.000000, 1.000000)
2 (-0.111111, 0.444444)
3 (0.074074, 0.074074)
4 (-0.008230, 0.032922)
5 (0.005487, 0.005487)
6 (-0.000610, 0.002439)
7 (0.000406, 0.000406)
8 (-0.000045, 0.000181)

参考文献
#

  1. 最优化理论与算法 第二版・陈宝林
  2. Gradient descent - wikipedia
并查集 → ←
comments powered by Disqus